$\begingroup$ The doubleangle formula for tangent would probably be helpful Do you know it?Trigonometric Simplification Calculator \square! The doubleangle formulas are summarized as follows sin(2θ) = 2sinθcosθ cos(2θ) = cos2θ − sin2θ = 1 − 2sin2θ = 2cos2θ − 1 tan(2θ) = 2tanθ 1 − tan2θ How to Given the tangent of an angle and the quadrant in which it is located, use the doubleangle formulas
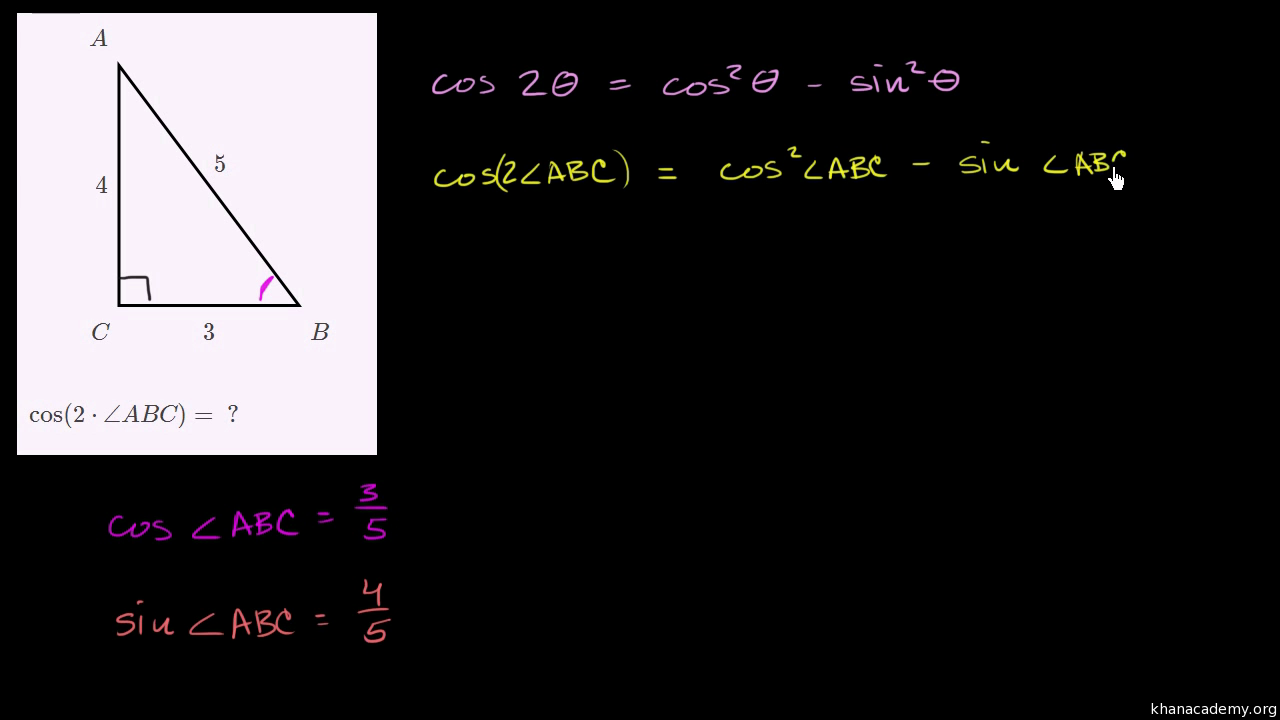
Double Angle Formulas Using Cosine Double Angle Identity Video Khan Academy
Tan 2x double angle formula
Tan 2x double angle formula-The angle in the sin double angle formula can be denoted by any symbol Therefore, the following three are popular forms of sine of double angle identity in terms of tangent (1) sin 2 x = 2 tan2 Find the value of the unknown angle 3 Once you find the value of your angle, subtract it from 180° to find the possible second angle 4 Add the new angle to the original angle If their sum is less than 180°, you have two valid answers If the sum is over 180°, then the second angle
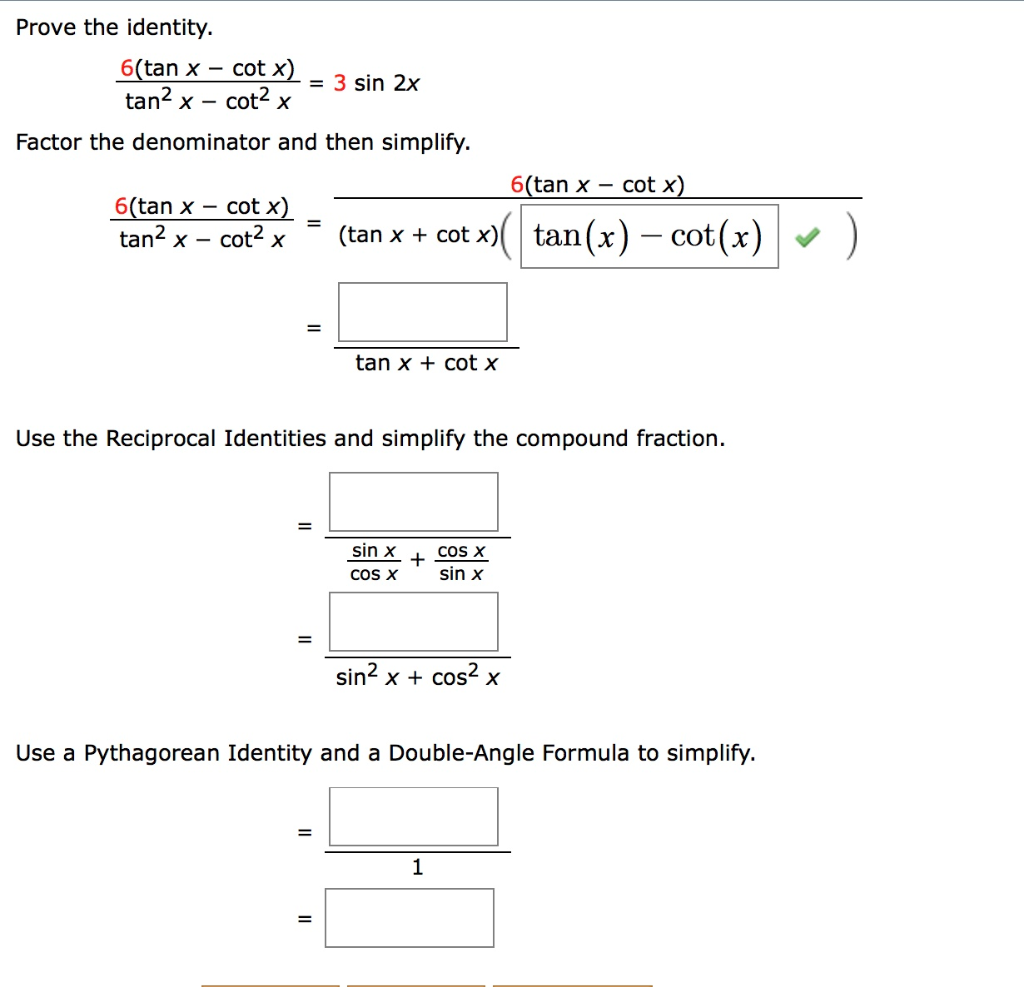



Prove The Identity 6 Tan X Cot X Tan2 X Cot2 X Chegg Com
The figure at the right shows a sector of a circle with radius 1 The sector is θ/(2 π) of the whole circle, so its area is θ/2We assume here that θ < π /2 = = = = The area of triangle OAD is AB/2, or sin(θ)/2The area of triangle OCD is CD/2, or tan(θ)/2 Since triangle OAD lies completely inside the sector, which in turn lies completely inside triangle OCD, we have2x 3x formula Proving Double angle formulas You are here Triple angle formulas Half angle formulas (Power reducing formulas) Ex 33, 24 Ex 33, 25 Ex 33, 23$\endgroup$ – Mike Pierce Dec '15 at 1712 $\begingroup$ @MikePierce It is not provided in my textbook, so it probably wants me to solve it without it $\endgroup$ –
The formulas for double angle identities are as follows If given one trigonometric function, its value, and its quadrant, you can find the exact value of every double angle identity For example, if told to find the exact value of sin2u given $\text {sec (u)}=\frac {9} {2}$, for $0\leq\text {u}\leq\frac {\pi} {2}$ (u is in quadrant 1) You mayFormula for Lowering Power tan^2 (x)=? To find the value of sin2x × Cos 2x, the trigonometric double angle formulas are used For the derivation, the values of sin 2x and cos 2x are used So, Sin 2x Cos 2x = 2 Cos x (2 Sin x Cos2 x − Sin x)
Trigonometric Formulas like Sin 2x, Cos 2x, Tan 2x are known as double angle formulas because these formulas have double angles in their trigonometric functions Let's discuss Tan2x Formula Tan2x Formula = 2 tan x 1 − t a n 2 x Let's know how to derive the double angle tan2x formulaAnswer to Double Angle Formulas Find sin 2x, cos 2x, and tan 2x from the given information, x in Quadrant IICos 2x ≠ 2 cos x;



Trig Find Tan X Given Tan 2x 2 Pi X 3pi 2 Cheatatmathhomework



2
Verify the identity 1 cos 2x tan x = sin 2x Use the appropriate doubleangle formulas to rewrite the numerator and dena simplified 1 cos 2x sin 2x 1 Simplify the numerator Enter denominator found in the previ The expression from the previous step then simplifies to tan x using what?For example, using these formulas we can transform an expression with exponents to one without exponents, but whose angles are multiples of the original angle We obtain halfangle formulas from double angle formulas Both sin (2A) and cos (2A) are derived from the double angle formula for the cosine cos (2A) = cos 2 (A) − sin 2 (A) = cos 2 The double angle formula, is the method of expressing Sin 2x, Cos 2x, and Tan 2x in congruent relationships with each other In this lesson, we will seek to prove on a



Double Angle Formula And Half Angle Formula Video Lessons Examples And Solutions
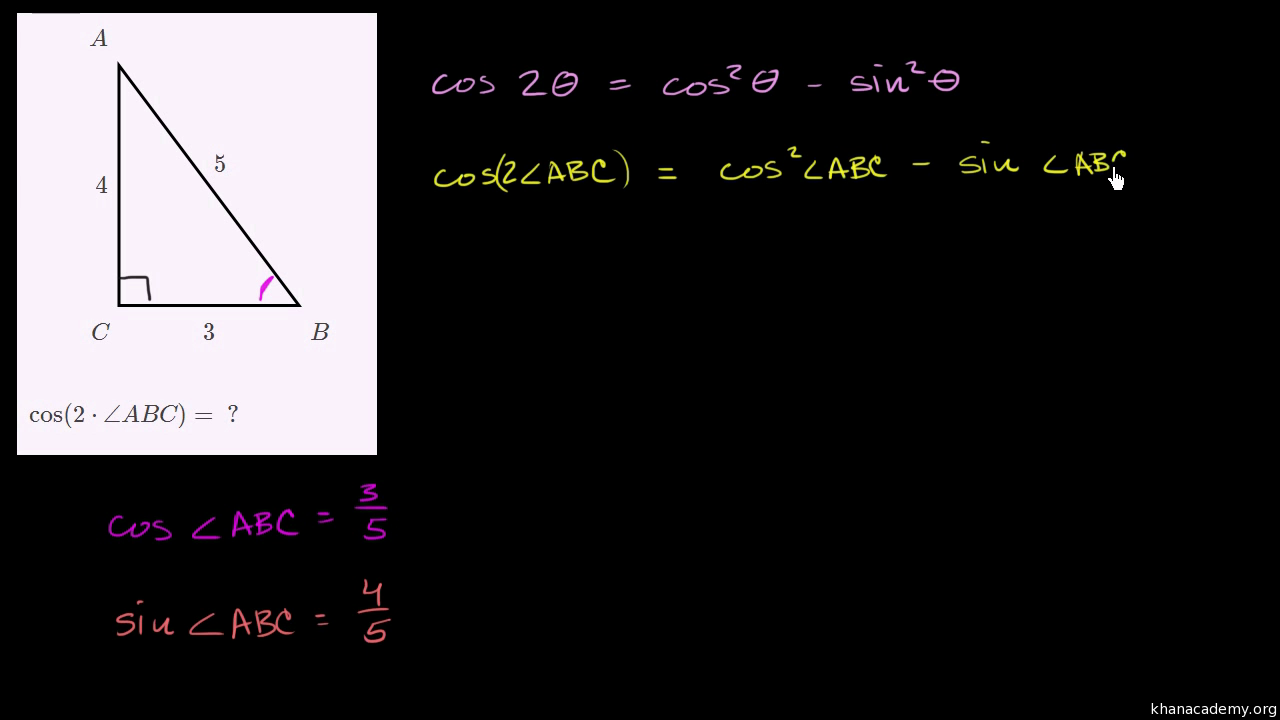



Double Angle Formulas Using Cosine Double Angle Identity Video Khan Academy
Formulas expressing trigonometric functions of an angle 2x in terms of functions of an angle x, sin(2x) = 2sinxcosx (1) cos(2x) = cos^2xsin^2x (2) = 2cos^2x1 (3) = 12sin^2x (4) tan(2x) = (2tanx)/(1tan^2x) (5) The corresponding hyperbolic function doubleangle formulas are sinh(2x) = 2sinhxcoshx (6) cosh(2x) = 2cosh^2x1 (7) tanh(2x) = (2tanhx)/(1tanh^2x)Tan 2x ≠ 2 tan x by Shavana GonzalezProof sin^2 (x)= (1cos2x)/2 Proof cos^2 (x)= (1cos2x)/2 Proof Half Angle Formula sin (x/2)




How To Write Double Angle Formula Sin 2x In Terms Of Tan X Youtube



2
Now, sin(2x) is 2sin(x)×cos(x), that's the double angle formula for sine00 Of course, you find that out from the addition formula09 Cos(2x) is cos 2 (x)sin 2 (x), that was the first double angle formula for cosine02 Now, it's not totally obvious how to proceed next, but I know that I'm trying to get everything in terms of tan(x)0844The tangent of half of an acute angle of a right triangle whose sides are a Pythagorean triple will necessarily be a rational number in the interval (0, 1) Vice versa, when a halfangle tangent is a rational number in the interval (0, 1), there is a right triangle that has the full angle and that has side lengths that are a Pythagorean tripleIt is called tan double angle identity and used as a formula in two cases Tan of double angle is expanded as the quotient of twice the tan function by subtraction of square of tan function from one The quotient of twice the tan function by subtraction of square of tan function from one is simplified as tan of double angle



Http Www Mayfieldschools Org Downloads 4 8 double angle formulas key Pdf




Double Angle Formula And Half Angle Formula Video Lessons Examples And Solutions
Expand tan (4x) tan (4x) tan ( 4 x) Factor 2 2 out of 4x 4 x tan(2(2x)) tan ( 2 ( 2 x)) Simplify the numerator Tap for more steps Apply the tangent double angle identity 2 2 tan ( x) 1 − tan 2 ( x) 1 − tan 2 ( 2 x) 2 2 tan ( x) 1 tan 2 ( x) 1 tan 2 ( 2 x) Simplify the denominator higher multiples 3A, 4A, and so on Tangent of a Double Angle To get the formula for tan 2A, you can either start with equation 50and put B = A to get tan(A A), or useO A Pythagorean Identity OB Quotient Identity OC




Double Angle And Half Angle Identities Lecture Notes Math 1b Docsity




Ppt Double Angle And Half Angle Formulas Powerpoint Presentation Free Download Id
Double angle formula for tangent tan2x = 2tanx/1tan^2x Formula for arc length= 1 – 2 sin2 x = 2 cos2 x – 1 • Tangent tan 2x = 2 tan x/1 tan2 x = 2 cot x/ cot2 x 1 = 2/cot x – tan x tangent doubleangle identity can be accomplished by applying the same methods, instead use the sum identity for tangent, first • Note sin 2x ≠ 2 sin x;Double angle formulas We can prove the double angle identities using the sum formulas for sine and cosine From these formulas, we also have the following identities sin 2 x = 1 2 ( 1 − cos 2 x) cos 2 x = 1 2 ( 1 cos 2 x) sin x cos x = 1 2 ( sin 2 x) tan 2 x = 1 − cos 2 x 1 cos 2 x




Sin 2 X Identities Regan Cletus




5 Tan 2x Cos 2x 2cos2x 9 Find Cos4x Iit Jee Trigonometry Double Angle Youtube
Tan2x Formula Tan2x Formula Sin 2x, Cos 2x, Tan 2x is the trigonometric formulas which are called as double angle formulas because they have double angles in their trigonometric functions Let's understand it by practicing it through solved example0/2 Points DETAILS PREVIOUS ANSWERS SPRECALC6 Find sin 2x, cos 2x, and tan 2x from the given information Functions sec x B x in Quadrant N X Symbols MY NOTES ASK YOUR TEACHER PRACTICE ANOTHER cale sin 2r = H q Relations Sets Simplify the expression by using a DoubleAngle Formula or a HalfAngle Formula Function cos 2r Vi o! Get an answer for 'verify (1 tan^2x)/(tan^2x) = csc^2x' and find homework help for other Math questions at eNotes Verify the identity `1/(tan^2x) 1/(cot^2x) = csc^2x sec^2x` 22tanx/1tan^2x YOU MIGHT ALSO LIKE Reciprocal, Quotient, and Pythagorean Identities 8 terms jessgac00 Trigonometric Identities some 35 terms baaskat000 trigometric identities Start



2



Http Www Humbleisd Net Cms Lib2 Tx Centricity Domain 2966 Chapter 9 1 9 4 notes key Pdf
Sum, difference, and double angle formulas for tangent The half angle formulas The ones for sine and cosine take the positive or negative square root depending on the quadrant of the angle θ/2 For example, if θ/2 is an acute angle, then the positive root would be used Truly obscure identities These are just here for perversity No, notConsider the expression sin3x We will use the addition formulae and double angle formulae to write this in a different form using only terms involving sinx and its powers We begin by thinking of 3x as 2xx and then using an addition formula wwwmathcentreacuk 3 c mathcentre 09Derivation of the Double Angle Formulas The Double Angle Formulas can be derived from Sum of Two Angles listed below $\sin (A B) = \sin A \, \cos B \cos A \, \sin B$ → Equation (1)




Ppt Analytic Trig Powerpoint Presentation Free Download Id
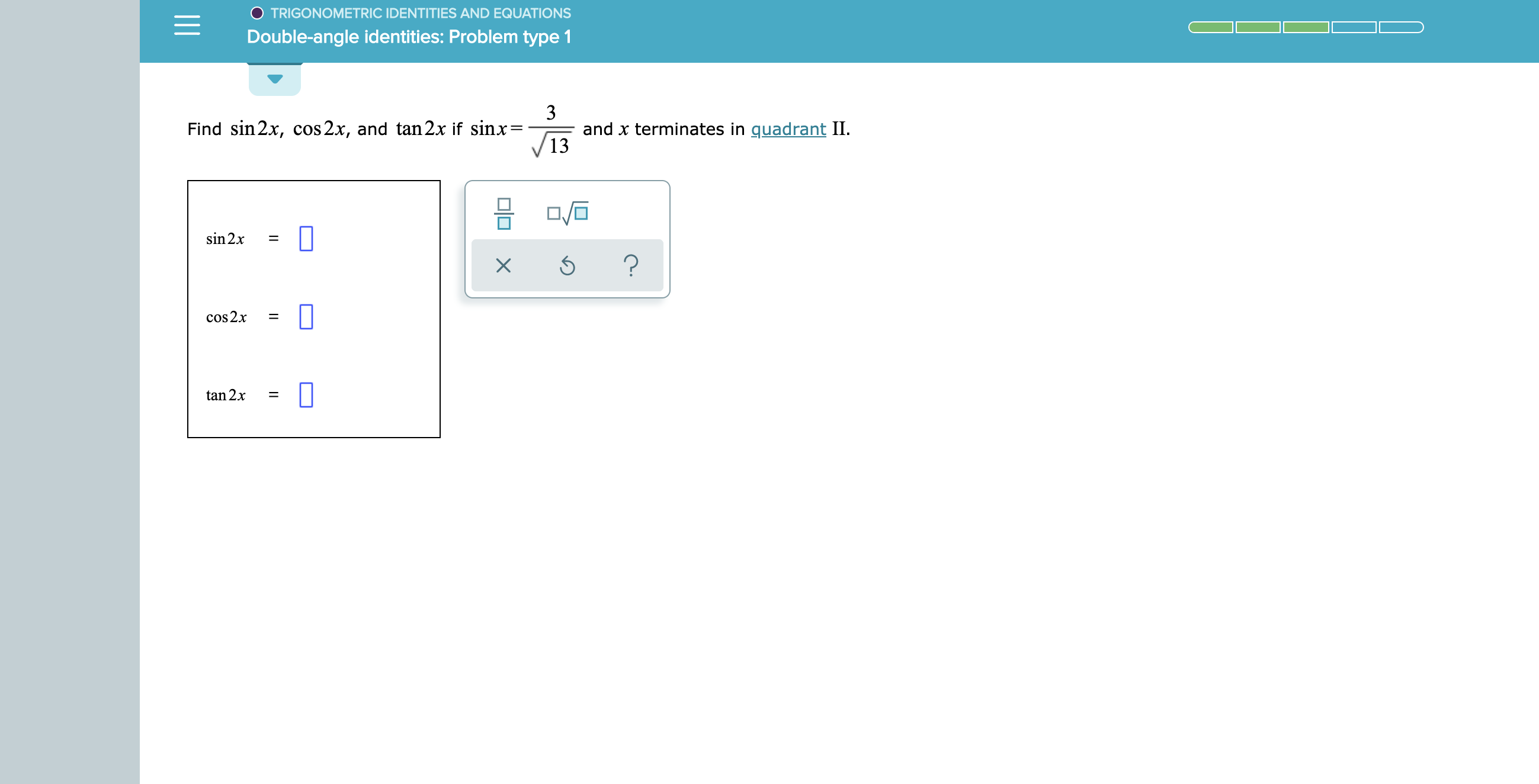



Answered Trigonometric Identities And Equations Bartleby
Learn how use the double angle identities to solve trigonometric equations When we have equations with a double angle we will apply the identities to creatThe trigonometric formulas like Sin2x, Cos 2x, Tan 2x are known as double angle formulae To understand this better, It is important to go through the practice examples provided Go through this article, and you will be able to derive the double angle formulae using the addition formulaeCombining this formula with the Pythagorean Identity, cos 2 (x) sin 2 (x) = 1, two other forms appear cos(2x) = 2cos 2 (x) − 1 and cos(2x ) = 1 − 2sin 2 (x) The derivation of the double angle identities for sine and cosine, followed by some examples



Leearlington Weebly Com Uploads 2 3 9 6 Precalculus Lesson 7 3c Pdf




Prove The Identity 4 Tan 3x 12 Tan X 4 Tan 3 Chegg Com
The double angle formulas can be derived by setting A = B in the sum formulas above For example, sin(2A) = sin(A)cos(A) cos(A)sin(A) = 2sin(A)cos(A) It is common to see two other forms expressing cos(2A) in terms of the sine and cosine of the single angle A Recall the square identity sin 2 (x) cos 2 (x) = 1 from Sections 14 and 23Problem Set 53 Double Angle, Half Angle, and Reduction Formulas 1 Explain how to determine the reduction identities from the doubleangle identity cos(2x) = cos2x−sin2x cos ( 2 x) = cos 2 x − sin 2 x 2 Explain how to determine the doubleangle formula for tan(2x) tan ( 2 x) using the doubleangle formulas for cos(2x) cos This result is called the sine of a double angle It is useful for simplifying expressions later Cosine of a Double Angle Using a similar process, we obtain the cosine of a double angle formula cos 2α = cos 2 α − sin 2 α Proof This time we start with the cosine of the sum of two angles cos(α β) = cos α cos β − sin α sin β,




Double Angle And Half Angle Formulas Ppt Download
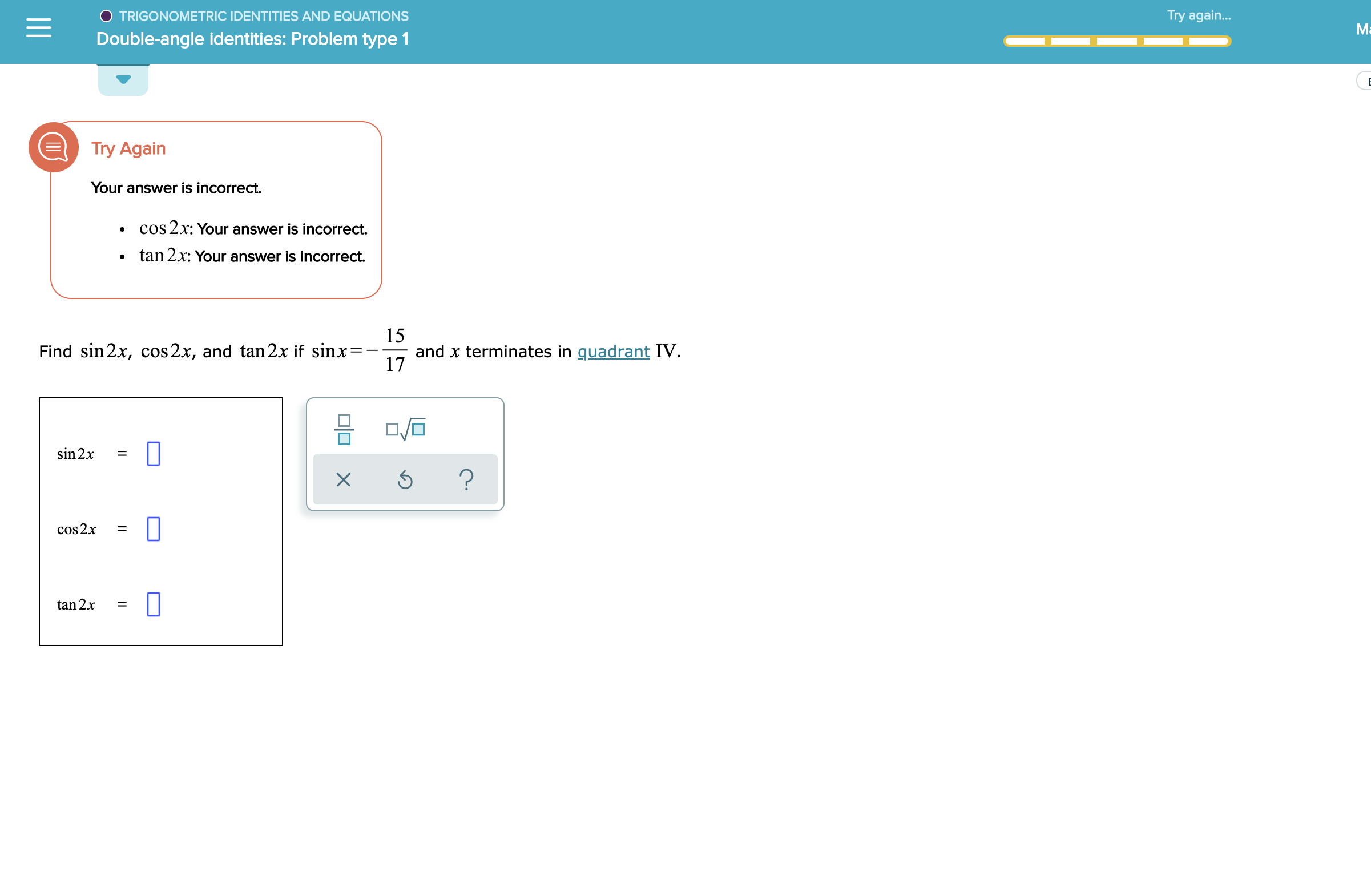



Answered O Trigonometric Identities And Bartleby
= cos 2 x – 1 cos 2 x = 2cos 2 x – 1 For tan 2x Next Triple angle formulas→ Concept wise; The sine of 60 is (root 3) / 2 This is why your friend sine is so upset Let's test our double angle formula with the same angle So sin (2 x) is sin60 For our double angle formulaThe trigonometric formulas like Sin2x, Cos 2x, Tan 2x are popular as double angle formulae, because they have double angles in their trigonometric functions For solving many problems we may use these widely The Sin 2x formula is \(Sin 2x = 2 sin x cos x\) Where x is the angle




1 Sin 2 X Formula Sepertikisahku




Ppt Double Angle And Half Angle Formulas Powerpoint Presentation Free Download Id
8 Given tan x= 7 find the exact value of tan 2x You must use a doubleangle formula Show all work Write your work on paper, take pictures and submit them in Blackboard Question 8 Given tan x= 7 find the exact value of tan 2x You must use a doubleangle formula Using the double angle identity for cosine cos 2 x = cos 2 x − sin 2 x cos 2 x = ( 1 − sin 2 x) − sin 2 x cos 2 x = 1 − 2 sin 2 x This expression is an equivalent expression to the double angle identity and is often considered an alternate form Example 342 5 Simplify the following identity sin 4 x − cos 4 x Double Angle Formulas The trigonometric double angle formulas give a relationship between the basic trigonometric functions applied to twice an angle in terms of trigonometric functions of the angle itself Tips for remembering the following formulas We can substitute the values ( 2 x) (2x) (2x) into the sum formulas for sin \sin sin and



Http Www Cbsd Org Cms Lib010 Pa Centricity Domain 40 5 5 double angle formulas Pdf
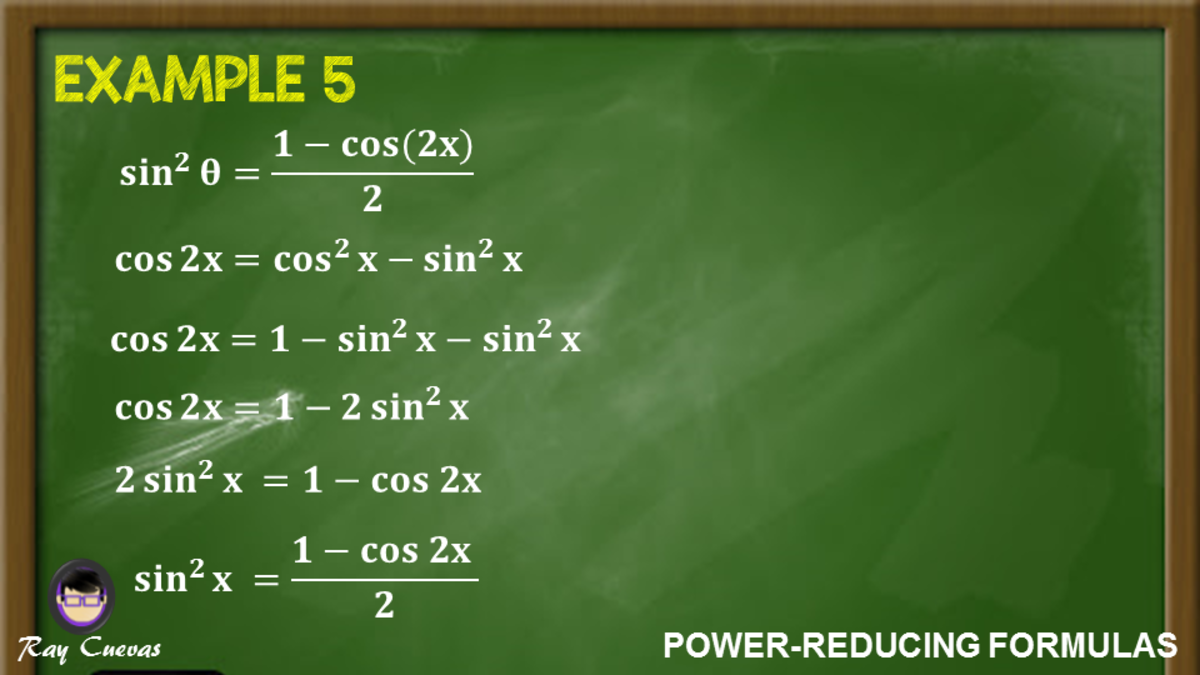



Power Reducing Formulas And How To Use Them With Examples Owlcation
Use tan x=sinx/cos x, sin 2x = 2 sin x cos x and cos 2x = cos^2xsin^2x, for the right hand side expression 2 tan x/(1tan^2x)=(2sin x/cos x)/(1(sin^2x/cos^2x) =2 sin x cos x/(cos^2xsin^2x) =(sin 2x)/(cos 2x)=tan 2x Proofs for sin 2x = 2 sin x cos x and cos 2x = 1 2 sin^2x Use Area of a triangleABC = 1/2(base)(altitude) = 1/2 bc sin A Here, it is the triangle ABC of a unitGet stepbystep solutions from expert tutors as fast as 1530 minutes Your first 5 questions are on us!Following table gives the double angle identities which can be used while solving the equations You can also have sin2θ,cos2θ expressed in terms of tanθ as under sin2θ = 2tanθ 1




Prove The Identity 6 Tan X Cot X Tan2 X Cot2 X Chegg Com




Double Angle Formula Sine Cosine And Tangent Owlcation



Q Tbn And9gcsxz Hkczzvj4wy3gx0dbnqphk3hi Cp Rmi Vgbp2veivzqwuc Usqp Cau




Lesson 52 Double Angle Half Angle Identities Ppt Download



Wl Apsva Us Wp Content Uploads Sites 38 15 05 Lesson 6 4 Notes 1 Pdf




Tan 2x Tan 2x




Prove Trigonometric Identity Using Double Angle Formula Youtube




Section 5 5 Multiple Angle And Half Angle Formulas



Http People Clas Ufl Edu Chui Files F13l3 Trig Integrals Part I Pdf
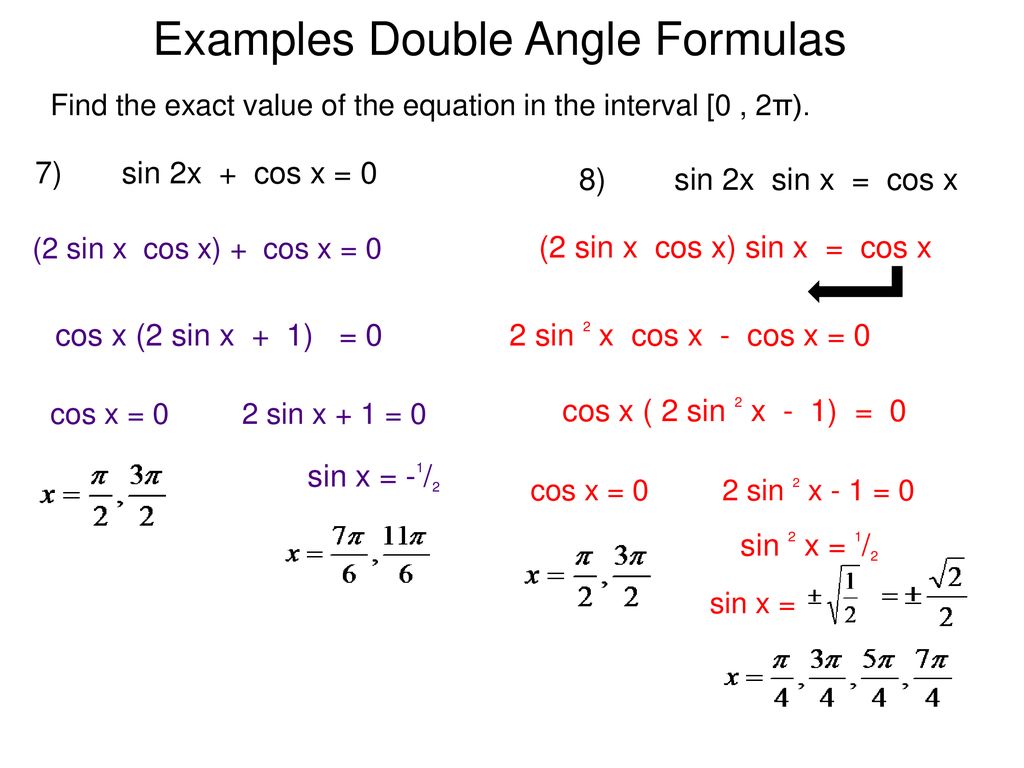



Examples Double Angle Formulas Ppt Download
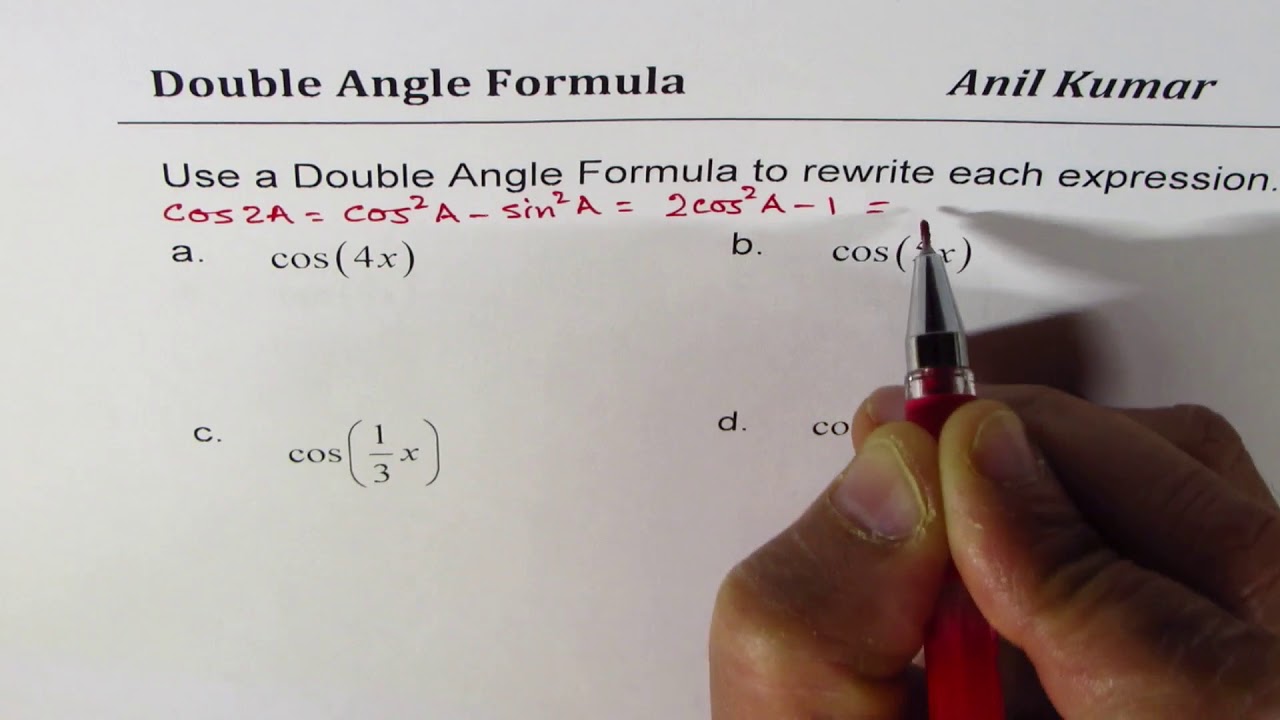



Cos 4x Sin 3x Tan X 2 Use Double Angle To Rewrite Trigonometric Expressions Youtube




7 3 Da Ha Red Sine Trigonometric Functions




Trig Angle Addition Identities Video Khan Academy




9 3 Other Identities Ppt Download




Half Angle Identities




Half Angle Formulas Power Reducing Formulas 2x 3x Formula Provin
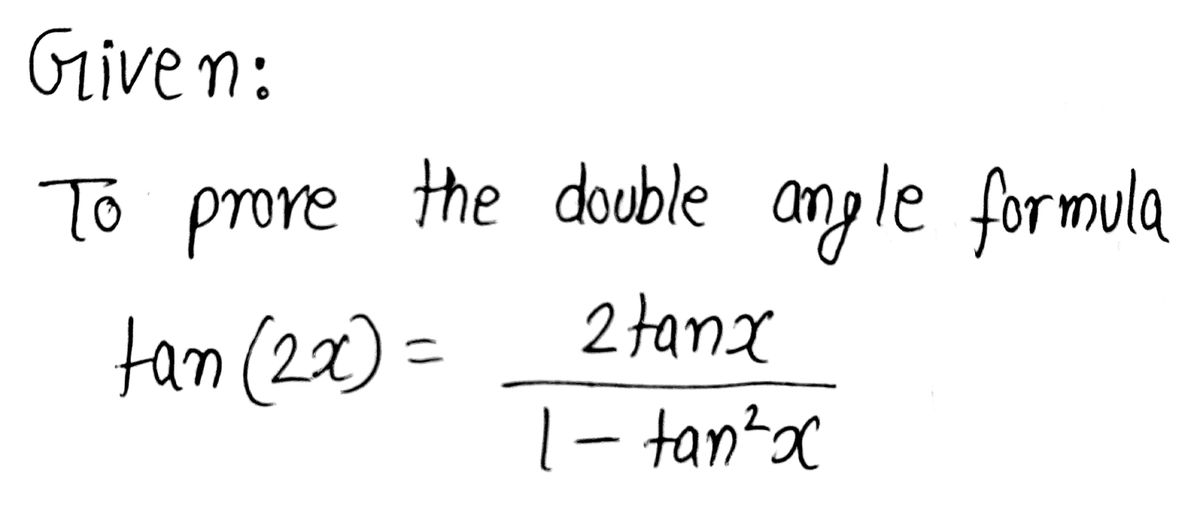



Answered Can You Guide Me Though The Proof Of Bartleby




Double Angle Formulas Sin 2x Cos 2x Tan 2x Trigonometry Creata Classes Youtube



2



2




Quiz Worksheet Double Angle Formula Study Com



Http Www Fortbendisd Com Cms Lib09 Tx Centricity Domain 7344 Double angle identities answer key Pdf



1




Double Angle Formula Tan Youtube




Solving Trigonometric Equations Ppt Download




Section 6 3 Double Angle And Half



Http Theprofessorshut Weebly Com Uploads 2 3 2 7 Pc Chap 6 Sect 3 Double And Half Angle Identities Pdf




Prove Each Of The Following Identities Use The Sum Chegg Com




3 4 2 Double Angle Identities K12 Libretexts




Chapter8 Circles 2 Pages 251 300 Flip Pdf Download Fliphtml5
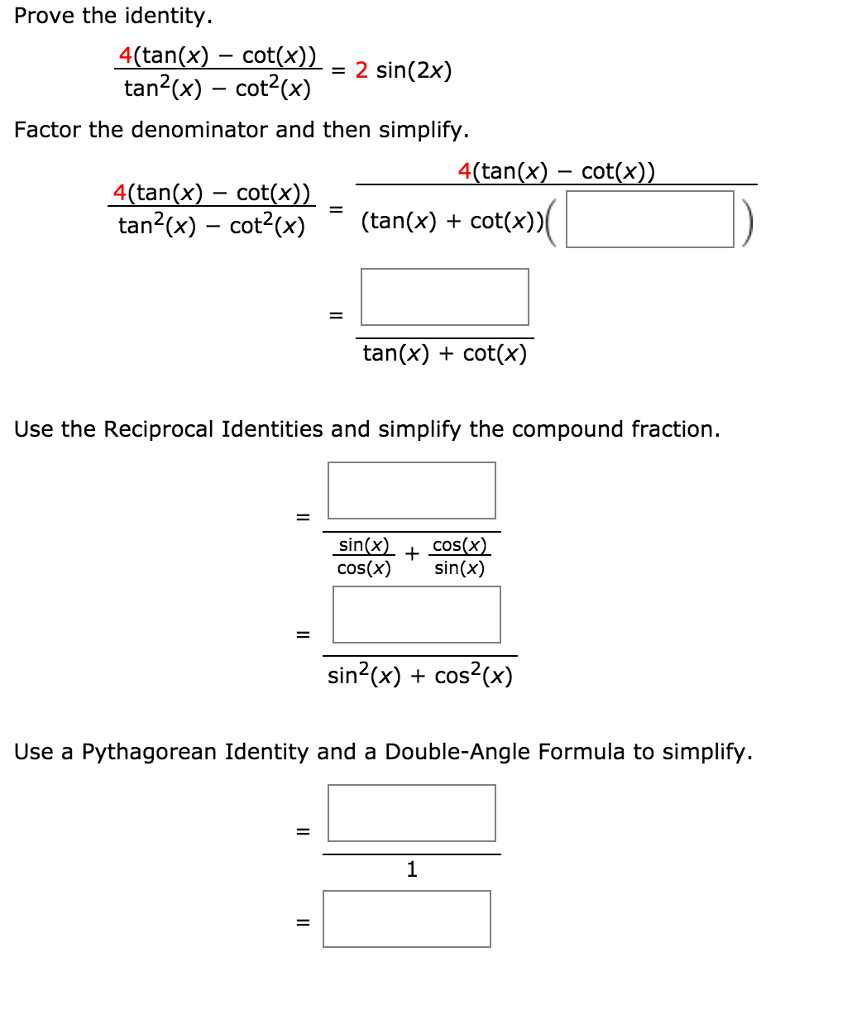



Prove The Identity 4 Tan X Cot X Tan 2 X Chegg Com



Double Angle Formula Sine Cosine And Tangent Owlcation




Tan2x Tan 2x Identity For Tan2x Proof Of Tan2x Identity Formula For Tan2x Youtube




Lesson 4 5 Double Angle Formulas




Trigonometric Identities Ppt Download



2




Ppt Double Angle And Half Angle Identities Powerpoint Presentation Free Download Id



7 4 Double Angle And Half Angle Identities Flip Ebook Pages 1 2 Anyflip Anyflip




3 Use Double Angle Formulas To Find The Exact Value Chegg Com




Find Sin 2x Cos 2x And Tan 2x If Tan X 3 And X Gauthmath




Derivative Rules For Trigonometric Functions



Www Rusdlearns Net C File Show




Examples Double Angle Formulas Ppt Download




Pre Calculus Using The Double Angle Of Tangent To Solve An Equation Youtube
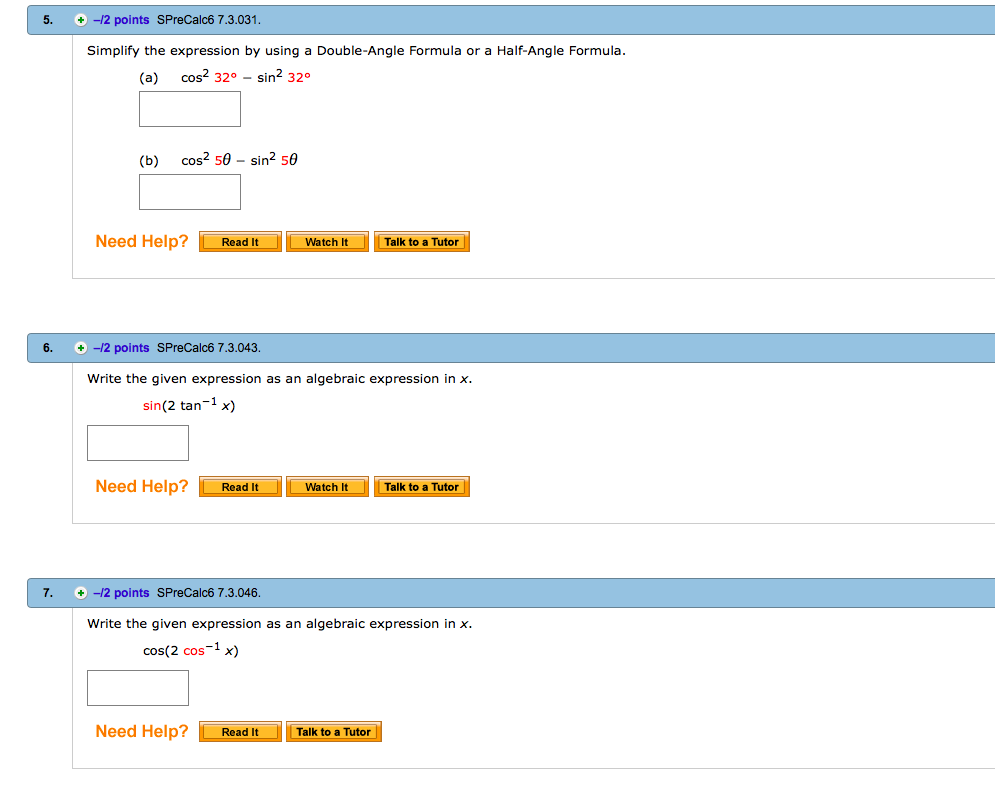



1 14 Points Sprecalc6 7 3 004 Find Sin 2x Cos 2x Chegg Com



Http Www Cbsd Org Cms Lib Pa Centricity Domain 40 5 5 double and half angle formulas notes Pdf
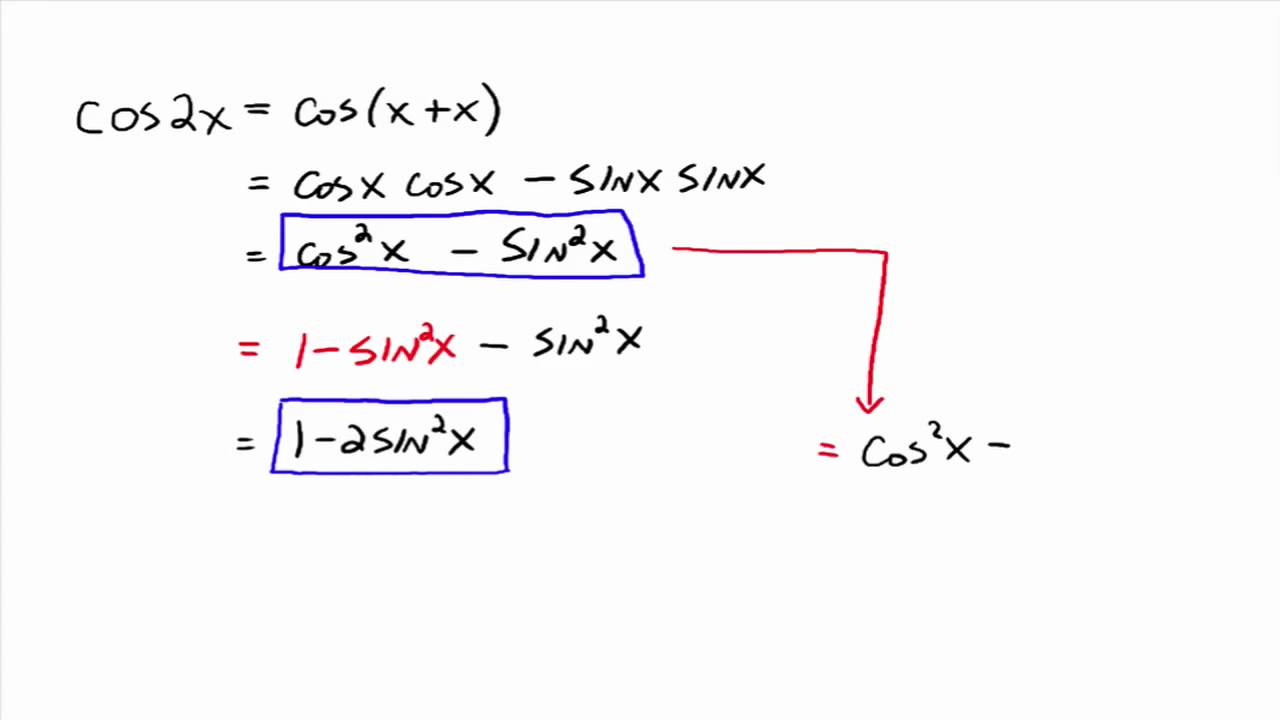



Double Angle Formula And Half Angle Formula Video Lessons Examples And Solutions



Http Www Anderson1 K12 Sc Us Cms Lib04 Sc Centricity Domain 1150 S15 hpc trig review keys Pdf




Trigonometric Identities And Formulas V2 0 Trigonometric Functions Sine



1




Trigonometric Identities Trigonometric Functions Trigonometry




Math2412 Double Angle Power Reducing Half Angle Identities Pdf Trigonometric Functions Sine



1
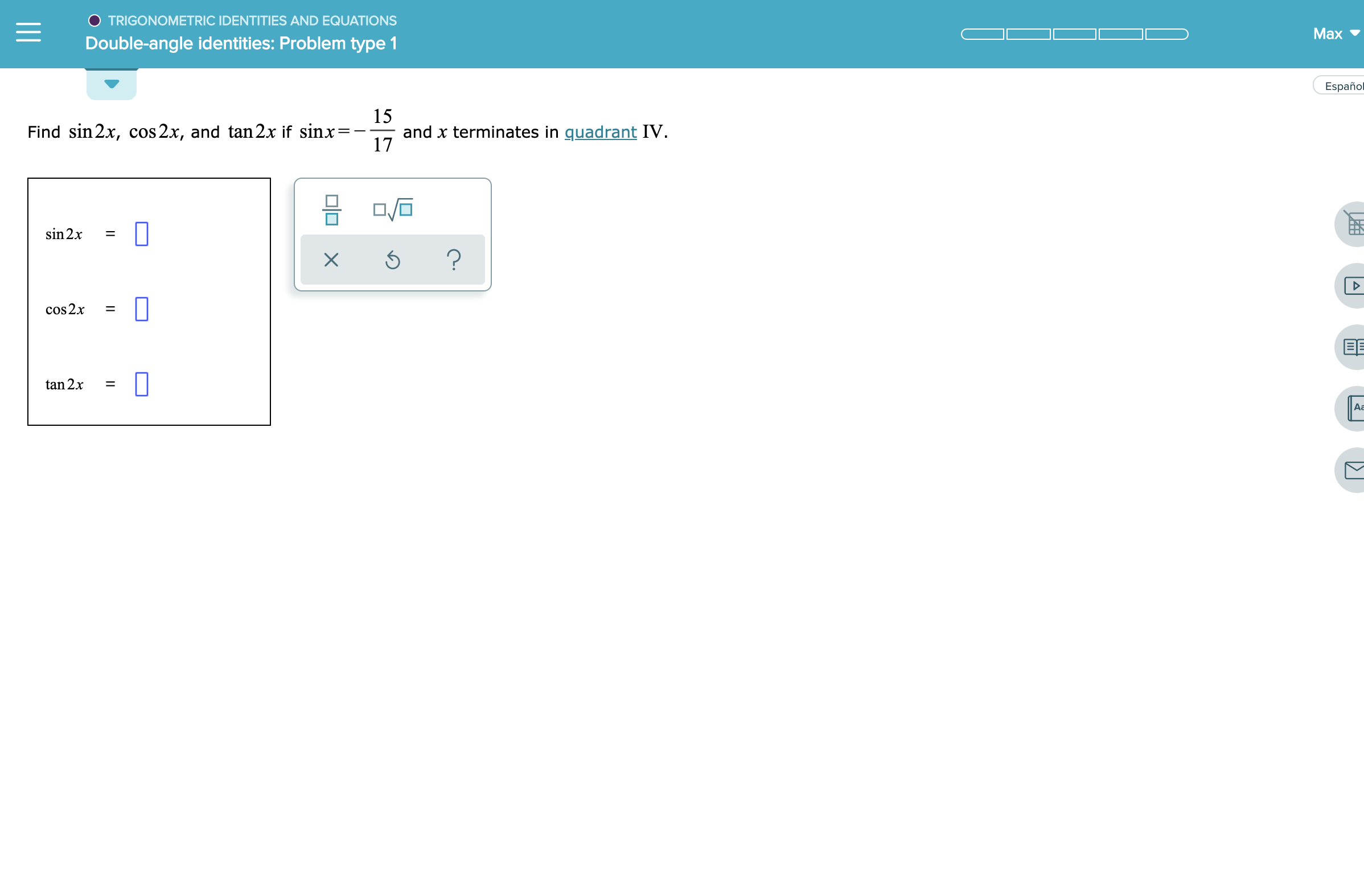



Answered O Trigonometric Identities And Bartleby
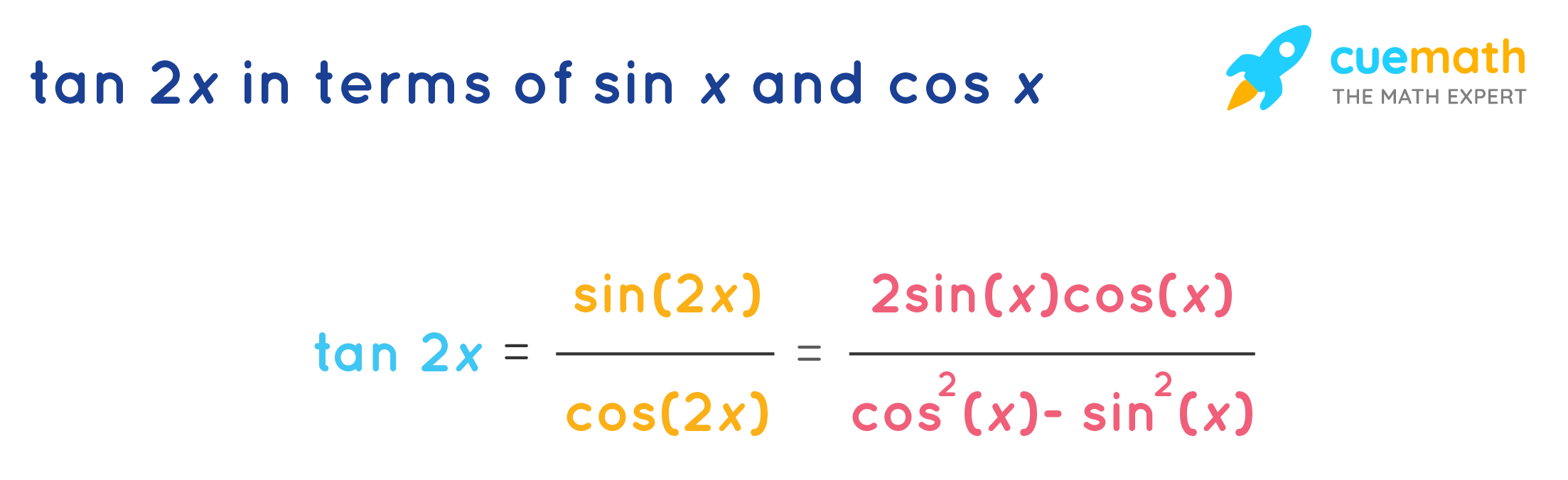



Tan 2x Formula What Is Tan 2x Formula Examples




Ppt Double Angle And Half Angle Formulas Powerpoint Presentation Free Download Id




Double Angle Formula Sine Cosine And Tangent Owlcation
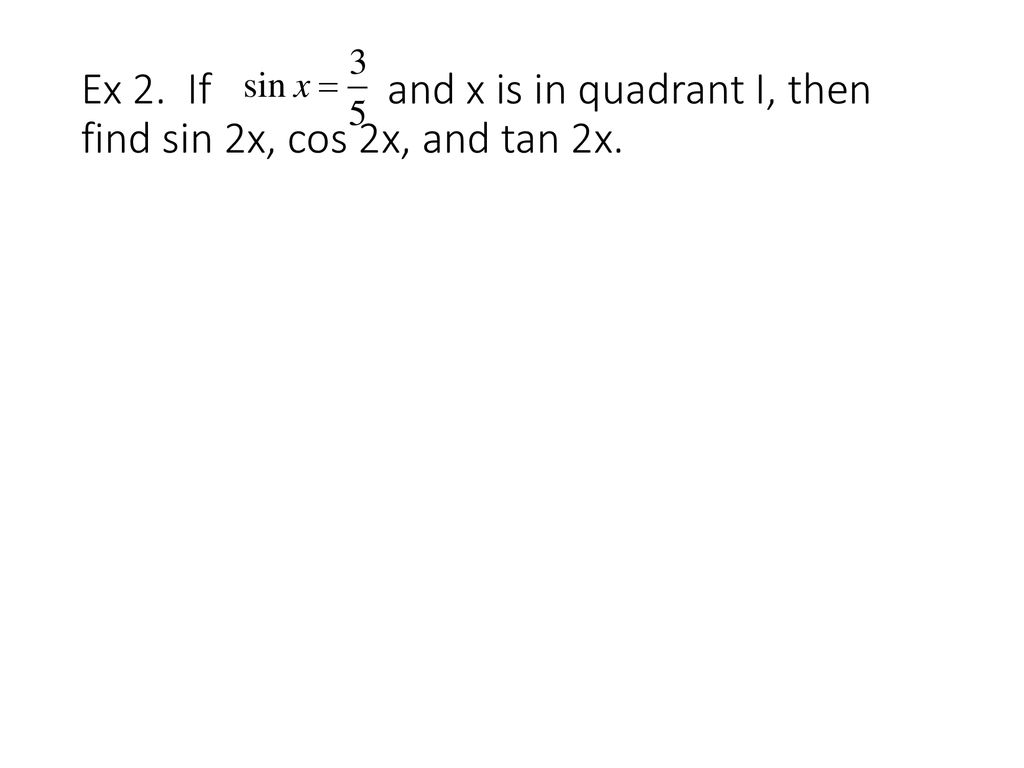



Double Angle Half Angle Formulas Ppt Download



2




Answered 4 Find The Exact Value Do Not Use A Bartleby




Double Angle Formulas What Are Double Angle Formulas Examples
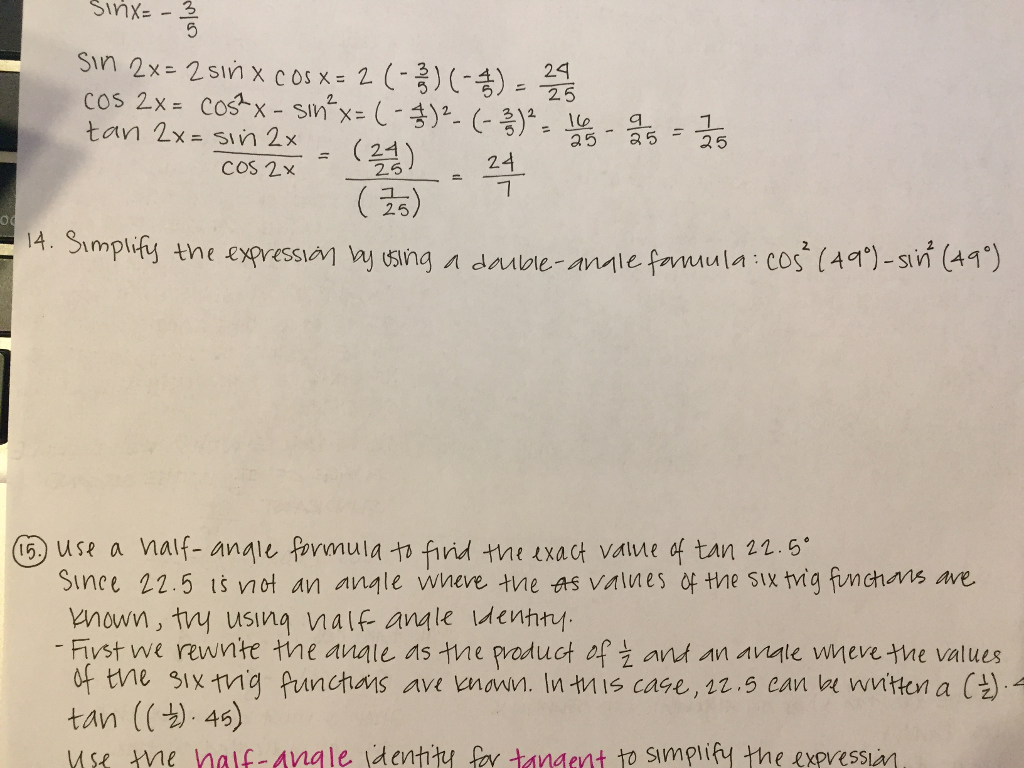



Solved Simplify The Expression Using The Double Angle For Chegg Com




Cosx 3 5 Find Tanx 2 Half Angle Tangent Formula Derivation With Important Example Youtube




Lecture 129 Proof Half Angle Formula Tan X 2 Cosmolearning Mathematics
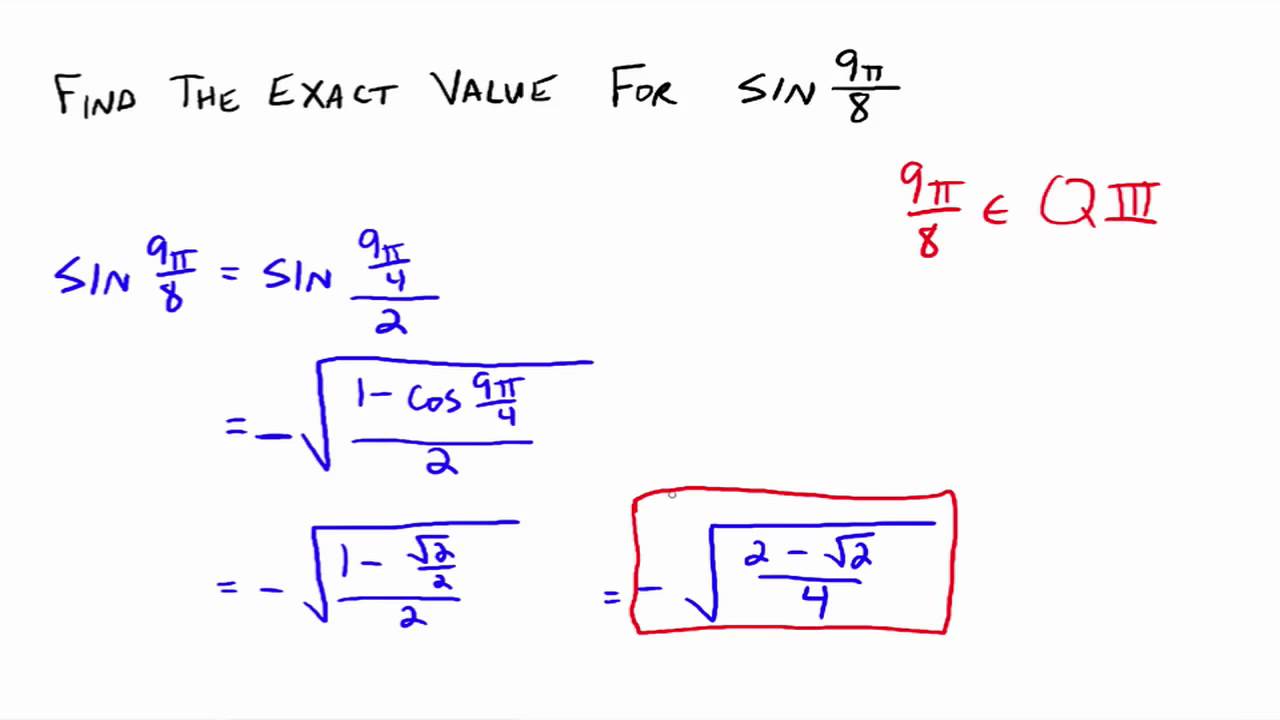



Double Angle And Half Angle Formulas With Worked Solutions Videos



Www Jensenmath Ca Unit 5 pretest review solutions Pdf




Section 7 3 Double Angle Half Angle And Sum




Ppt Find Sin 2x Cos 2x And Tan 2x From The Given Information Image Select The Correct Answer Powerpoint Presentation Id




Double Angle Half Angle Formulas Ppt Download




Tan 2x Formula What Is Tan 2x Formula Examples



Web Stanford Edu Class Archive Math Math Math 1144 Files Trig Pdf




Double Angle Identities Formula In Trigonometry In Hindi Urdu Full Hd Youtube




56 Questions On Double Angle And Half Angle Formula Precalculus Math 1330 Docsity




3 4 2 Double Angle Identities K12 Libretexts
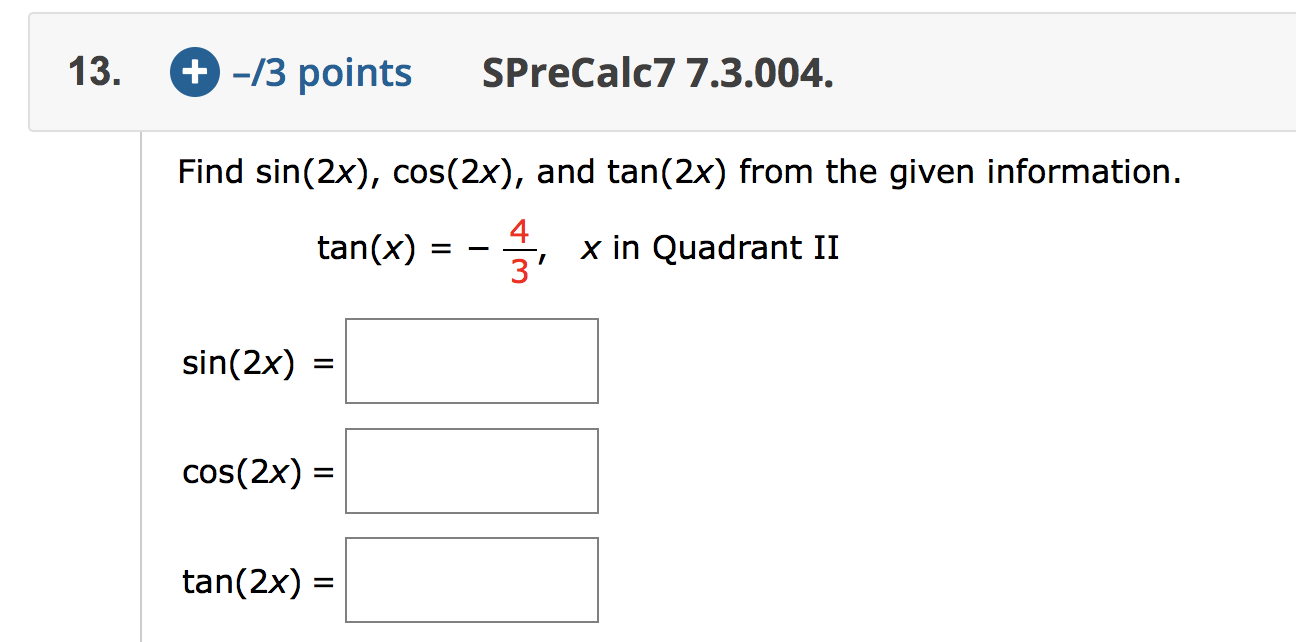



2 Points Sprecalc7 7 3 029 16 Simplify The Chegg Com




Section 7 3 Double Angle Half Angle And Chegg Com




Calculate Sin2x Cos2x And Tan2x For Given Tanx In Quadrant 2 Youtube



Http Www Pstcc Edu Facstaff Jwlamb 1730 7 3 Pdf



Wl Apsva Us Wp Content Uploads Sites 38 15 05 Lesson 6 4 Notes 1 Pdf




1 Sin 2 0 Cos 2x 1 Tan 3 To Prove That 1 Tan 2 Chegg Com



0 件のコメント:
コメントを投稿